حل حجم یک شکل محدود شده با خطوط به صورت آنلاین. مساحت شکل محدود شده با خطوط را محاسبه کنید. کاربرد انتگرال برای حل مسائل کاربردی

ما متوجه شدیم که چگونه مساحت ذوزنقه منحنی G را پیدا کنیم. در اینجا فرمول های حاصل آمده است:
برای یک تابع پیوسته و غیر منفی y=f(x) روی قطعه،
برای یک تابع پیوسته و غیر مثبت y=f(x) روی قطعه.

با این حال، هنگام حل مسائل مربوط به یافتن منطقه، اغلب باید با ارقام پیچیده تری سر و کار داشته باشید.

در این مقاله در مورد محاسبه مساحت ارقامی صحبت خواهیم کرد که مرزهای آنها با توابع به طور صریح مشخص شده است، یعنی به صورت y=f(x) یا x=g(y) و به تفصیل حل نمونه های معمولی را تجزیه و تحلیل خواهیم کرد. مثال ها.

پیمایش صفحه.

فرمول محاسبه مساحت شکل محدود شده با خطوط y=f(x) یا x=g(y).

قضیه.

اجازه دهید توابع و در بازه تعریف شده و پیوسته باشند، و برای هر مقدار x از . سپس ناحیه شکل G محدود به خطوط x=a , x=b و با فرمول محاسبه می شود .

یک فرمول مشابه برای مساحت شکل محدود شده با خطوط y=c، y=d و: .

اثبات

اجازه دهید اعتبار فرمول را برای سه مورد نشان دهیم:

در حالت اول، وقتی هر دو تابع غیرمنفی هستند، به دلیل خاصیت افزایشی مساحت، مجموع مساحت شکل اصلی G و ذوزنقه منحنی برابر با مساحت شکل است. از این رو،

از همین رو، . آخرین انتقال به دلیل خاصیت سوم انتگرال معین امکان پذیر است.

به همین ترتیب، در مورد دوم برابری صادق است. در اینجا یک تصویر گرافیکی وجود دارد:

در حالت سوم، زمانی که هر دو تابع غیر مثبت هستند، داریم. بیایید این را نشان دهیم:

اکنون می‌توانیم به حالت کلی برویم که توابع محور Ox را قطع کنند.

بیایید نقاط تقاطع را نشان دهیم. این نقاط قطعه را به n قسمت تقسیم می کنند که در آن . شکل G را می توان با اتحادیه ای از شکل ها نشان داد . بدیهی است که در فاصله زمانی آن تحت یکی از سه مورد قبلاً در نظر گرفته شده قرار می گیرد، بنابراین مناطق آنها به صورت

از این رو،

آخرین انتقال به دلیل خاصیت پنجم انتگرال معین معتبر است.

تصویر گرافیکی مورد کلی.

بنابراین فرمول ثابت شده است.

وقت آن است که به سراغ حل نمونه هایی از پیدا کردن مساحت شکل های محدود شده با خطوط y=f(x) و x=g(y) برویم.

نمونه هایی از محاسبه مساحت یک شکل محدود شده با خطوط y=f(x) یا x=g(y).

حل هر مسئله را با ساختن یک شکل در یک هواپیما آغاز خواهیم کرد. این به ما این امکان را می دهد که یک شکل پیچیده را به عنوان ترکیبی از شکل های ساده تر تصور کنیم. اگر در ساخت و ساز مشکل دارید به مقالات مراجعه کنید: ; و .

مثال.

مساحت یک شکل محدود به سهمی را محاسبه کنید و خطوط مستقیم، x=1، x=4.

راه حل.

بیایید این خطوط را روی یک هواپیما رسم کنیم.

در همه جای قطعه نمودار سهمی است بالای خط مستقیم بنابراین، فرمول به دست آمده قبلی را برای مساحت اعمال می کنیم و انتگرال معین را با استفاده از فرمول نیوتن-لایب نیتس محاسبه می کنیم:

بیایید مثال را کمی پیچیده کنیم.

مثال.

مساحت شکل محدود شده با خطوط را محاسبه کنید.

راه حل.

این چه تفاوتی با نمونه های قبلی دارد؟ قبلا همیشه دو خط مستقیم داشتیم، موازی با محور abscissa، و اکنون فقط یک x=7 وجود دارد. بلافاصله این سؤال مطرح می شود: از کجا می توان حد دوم ادغام را بدست آورد؟ بیایید به نقاشی برای این نگاه کنیم.

مشخص شد که حد پایین ادغام هنگام یافتن مساحت یک شکل، آبسیسا نقطه تقاطع نمودار خط مستقیم y=x و نیمه سهمی است. ما این ابسیسا را ​​از برابری می یابیم:

بنابراین آبسیسا نقطه تقاطع x=2 است.

توجه داشته باشید.

در مثال ما و در نقاشی مشخص است که خطوط و y=x در نقطه (2;2) قطع می شوند و محاسبات قبلی غیر ضروری به نظر می رسند. اما در موارد دیگر، ممکن است همه چیز چندان واضح نباشد. بنابراین توصیه می کنیم همیشه ابسیساها و مختصات نقاط تلاقی خطوط را به صورت تحلیلی محاسبه کنید.

بدیهی است که نمودار تابع y=x در بالای نمودار تابع در بازه قرار دارد. برای محاسبه مساحت از فرمول استفاده می کنیم:

بیایید کار را حتی دشوارتر کنیم.

مثال.

مساحت شکل محدود شده با نمودار توابع و .

راه حل.

بیایید نموداری از نسبت معکوس و سهمی ها بسازیم .

قبل از اعمال فرمول برای یافتن مساحت یک شکل، باید در مورد محدودیت های ادغام تصمیم گیری کنیم. برای این کار، آبسیسا نقاط تلاقی خطوط را پیدا می کنیم، عبارات و .

برای مقادیر غیر صفر x، برابری معادل معادله درجه سوم است با ضرایب صحیح برای یادآوری الگوریتم حل آن می توانید به بخش مراجعه کنید.

به راحتی می توان بررسی کرد که x=1 ریشه این معادله است: .

با تقسیم عبارت برای دوجمله ای x-1 داریم:

بنابراین، ریشه های باقی مانده از معادله پیدا می شود :

اکنون از نقاشی مشخص شد که شکل G در بالای خط آبی و زیر خط قرمز در فاصله وجود دارد . بنابراین، مساحت مورد نیاز برابر خواهد بود

بیایید به یک مثال معمولی دیگر نگاه کنیم.

مثال.

مساحت شکل محدود شده با منحنی ها را محاسبه کنید و محور آبسیسا.

راه حل.

بیایید یک نقاشی بکشیم.

این یک تابع توان معمولی با توان یک سوم، نمودار تابع است می توان از نمودار با نمایش متقارن نسبت به محور x و بالا بردن آن توسط یک نمودار بدست آورد.

بیایید نقاط تقاطع همه خطوط را پیدا کنیم.

محور آبسیسا معادله y=0 را دارد.

نمودارهای توابع و y=0 در نقطه (0;0) قطع می شوند زیرا x=0 تنها ریشه واقعی معادله است.

نمودارهای تابع و y=0 در نقطه (2;0) قطع می شوند زیرا x=2 تنها ریشه معادله است. .

نمودار توابع و در نقطه (1;1) قطع می شوند زیرا x=1 تنها ریشه معادله است . این عبارت کاملاً واضح نیست، اما عملکرد به شدت در حال افزایش است، و - بنابراین، معادله به شدت کاهش می یابد حداکثر یک ریشه دارد.

تنها نکته: در این مورد، برای یافتن منطقه باید از فرمول فرم استفاده کنید . یعنی خطوط مرزی باید به عنوان توابع آرگومان نمایش داده شوند y و خط سیاه.

بیایید نقاط تلاقی خطوط را تعیین کنیم.

بیایید با نمودار توابع و:

بیایید نقطه تقاطع نمودار توابع را پیدا کنیم و:

باقی مانده است که نقطه تلاقی خطوط را پیدا کنیم و:

همانطور که می بینید، مقادیر یکسان هستند.

خلاصه کنید.

ما همه رایج ترین موارد پیدا کردن مساحت یک شکل را که با خطوط کاملاً مشخص محدود شده است تجزیه و تحلیل کرده ایم. برای انجام این کار، شما باید بتوانید خطوطی را در یک صفحه بسازید، نقاط تقاطع خطوط را پیدا کنید و فرمول را برای یافتن مساحت اعمال کنید، که حاکی از توانایی محاسبه انتگرال های خاص است.

در این درس محاسبه را یاد می گیریم مناطق شکل های هواپیماکه نامیده می شوند ذوزنقه های منحنی .

نمونه هایی از این شکل ها در شکل زیر آمده است.

از یک طرف، یافتن مساحت یک شکل صفحه با استفاده از یک انتگرال معین بسیار ساده است. ما در مورد مساحت یک شکل صحبت می کنیم که از بالا با یک منحنی خاص و از پایین توسط محور آبسیسا محدود می شود ( گاو نر) و در سمت چپ و راست چند خط مستقیم وجود دارد. سادگی آن است انتگرال قطعی تابعی که منحنی به آن داده می شود مساحت چنین شکلی است(ذوزنقه منحنی).

برای محاسبه مساحت یک شکل به موارد زیر نیاز داریم:

1. انتگرال معین تابعی که منحنی را تعریف می کند ، که ذوزنقه منحنی را از بالا محدود می کند. و در اینجا اولین تفاوت مهم ظاهر می شود: یک ذوزنقه منحنی را می توان با یک منحنی نه تنها از بالا، بلکه از پایین نیز محدود کرد . در این مورد چگونه باید اقدام کرد؟ ساده، اما مهم به خاطر سپردن: انتگرال در این مورد با علامت منفی گرفته می شود .
2. محدودیت های ادغام آو ب، که از معادلات خطوط محدود کننده شکل در سمت چپ و راست به دست می آوریم: ایکس = آ , ایکس = ب، جایی که آو ب- شماره.

به طور جداگانه، در مورد برخی تفاوت های ظریف دیگر.

منحنی که ذوزنقه منحنی را در بالا (یا پایین) محدود می کند باید باشد نمودار یک تابع پیوسته و غیر منفی y = f(ایکس) .

مقادیر "x" باید متعلق به بخش باشد [آ, ب] . یعنی خطوطی مانند برش قارچ در نظر گرفته نمی شود که ساقه آن به خوبی در این قسمت قرار می گیرد و کلاهک بسیار گسترده تر است.

بخش های جانبی می توانند به نقاطی تبدیل شوند . اگر چنین شکلی را در نقاشی می بینید، این نباید شما را گیج کند، زیرا این نقطه همیشه ارزش خود را در محور "x" دارد. این بدان معنی است که همه چیز با محدودیت های یکپارچگی مرتب است.

اکنون می توانید به سراغ فرمول ها و محاسبات بروید. بنابراین منطقه سذوزنقه منحنی را می توان با استفاده از فرمول محاسبه کرد

اگر f(ایکس) ≤ 0 (گراف تابع زیر محور قرار دارد گاو نر) آن ناحیه یک ذوزنقه منحنیرا می توان با استفاده از فرمول محاسبه کرد

همچنین مواردی وجود دارد که هر دو مرز بالایی و پایینی شکل به ترتیب تابع هستند y = f(ایکس) و y = φ (ایکس) ، سپس مساحت چنین رقمی با فرمول محاسبه می شود

. (3)

حل مشکلات با هم

بیایید با مواردی شروع کنیم که مساحت یک شکل را می توان با استفاده از فرمول (1) محاسبه کرد.

مثال 1.گاو نر) و مستقیم ایکس = 1 , ایکس = 3 .

راه حل. زیرا y = 1/ایکس> 0 در قطعه ، سپس مساحت ذوزنقه منحنی با استفاده از فرمول (1) پیدا می شود:

.

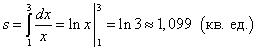مثال 2.مساحت شکل محدود شده با نمودار تابع، خط را پیدا کنید ایکس= 1 و محور x ( گاو نر ).

راه حل. نتیجه اعمال فرمول (1):

اگر پس از آن س= 1/2؛ اگر پس از آن س= 1/3 و غیره

مثال 3.مساحت شکل محدود شده با نمودار تابع، محور آبسیسا ( گاو نر) و مستقیم ایکس = 4 .

راه حل. شکل مربوط به شرایط مسئله یک ذوزنقه منحنی است که در آن قسمت سمت چپ به یک نقطه تبدیل شده است. حدود ادغام 0 و 4 است. از آنجایی که با استفاده از فرمول (1) مساحت ذوزنقه منحنی را پیدا می کنیم:

.

مثال 4.مساحت شکل محدود شده با خطوط، و واقع در ربع اول را بیابید.

راه حل. برای استفاده از فرمول (1)، بیایید مساحت شکل را که با شرایط مثال به دست آمده است به عنوان مجموع مساحت های مثلث تصور کنیم. OABو ذوزنقه منحنی ABC. هنگام محاسبه مساحت یک مثلث OABحدود ادغام، ابسیساهای نقاط هستند Oو آو برای شکل ABC- ابسیسا از نقاط آو سی (آنقطه تقاطع خط است O.A.و سهمی ها، و سی- نقطه تقاطع سهمی با محور گاو نر). با حل مشترک (به عنوان یک سیستم) معادلات یک خط مستقیم و یک سهمی، به (آبسیسا نقطه) می رسیم. آ) و (آبسیسا نقطه تلاقی دیگر خط و سهمی که برای حل مورد نیاز نیست). به طور مشابه، (مجموعه نقاط سیو دی). اکنون همه چیزهایی که برای یافتن مساحت یک شکل نیاز داریم در اختیار داریم. ما پیدا می کنیم:

مثال 5.مساحت ذوزنقه منحنی را پیدا کنید ACDB، اگر معادله منحنی باشد سی دیو آبسیسا آو ببه ترتیب 1 و 2.

راه حل. اجازه دهید این معادله منحنی را از طریق بازی بیان کنیم: مساحت ذوزنقه منحنی با استفاده از فرمول (1) پیدا می شود:

.

بیایید به مواردی برویم که مساحت یک شکل را می توان با استفاده از فرمول (2) محاسبه کرد.

مثال 6.مساحت شکل محدود شده با سهمی و محور x را بیابید ( گاو نر ).

راه حل. این شکل در زیر محور x قرار دارد. بنابراین برای محاسبه مساحت آن از فرمول (2) استفاده می کنیم. حدود ادغام آبسیسا و نقاط تقاطع سهمی با محور است. گاو نر. از این رو،

مثال 7.ناحیه محصور شده بین محور آبسیسا را ​​بیابید ( گاو نر) و دو موج سینوسی مجاور.

راه حل. مساحت این شکل را می توان با استفاده از فرمول (2) پیدا کرد:

.

بیایید هر اصطلاح را جداگانه پیدا کنیم:

.

.

سرانجام منطقه را پیدا می کنیم:

.

مثال 8.مساحت شکل محصور بین سهمی و منحنی را پیدا کنید.

راه حل. بیایید معادلات خطوط را از طریق بازی بیان کنیم:

مساحت طبق فرمول (2) به صورت به دست می آید

,

جایی که آو ب- ابسیسا از نقاط آو ب. بیایید آنها را با حل معادلات با هم پیدا کنیم:

سرانجام منطقه را پیدا می کنیم:

و در نهایت مواردی که می توان مساحت یک رقم را با استفاده از فرمول (3) محاسبه کرد.

مثال 9.مساحت شکل محصور در بین سهمی ها را پیدا کنید و .

محاسبه مساحت یک شکل- این شاید یکی از دشوارترین مسائل در نظریه منطقه باشد. در هندسه مدرسه به آنها آموزش داده می شود که مساحت اشکال هندسی اساسی مانند مثلث، لوزی، مستطیل، ذوزنقه، دایره و غیره را بیابند. با این حال، شما اغلب باید با محاسبه مساحت ارقام پیچیده تر سر و کار داشته باشید. هنگام حل چنین مسائلی است که استفاده از حساب انتگرال بسیار راحت است.

تعریف.

ذوزنقه منحنیمقداری از شکل G را که با خطوط y = f(x)، y = 0، x = a و x = b محدود شده است، فراخوانی کنید و تابع f(x) در قطعه [a; ب] و علامت آن را روی آن تغییر نمی دهد (عکس. 1).مساحت ذوزنقه منحنی را می توان با S(G) نشان داد.

یک انتگرال معین ʃ a b f(x)dx برای تابع f(x)، که در بازه [a; b]، و مساحت ذوزنقه منحنی مربوطه است.

یعنی برای یافتن مساحت یک شکل G محدود به خطوط y = f(x)، y = 0، x = a و x = b، لازم است انتگرال معین ʃ a b f(x)dx محاسبه شود. .

بدین ترتیب، S(G) = ʃ a b f(x)dx.

اگر تابع y = f(x) روی [a; b]، سپس مساحت ذوزنقه منحنی را می توان با استفاده از فرمول پیدا کرد S(G) = -ʃ a b f(x)dx.

مثال 1.

مساحت شکل محدود شده با خطوط y = x 3 را محاسبه کنید. y = 1; x = 2.

راه حل.

خطوط داده شده شکل ABC را تشکیل می دهند که با هچ کردن نشان داده می شود برنج. 2.

مساحت مورد نیاز برابر است با تفاوت بین مساحت ذوزنقه منحنی DACE و مربع DABE.

با استفاده از فرمول S = ʃ a b f(x)dx = S(b) – S(a)، حدود ادغام را پیدا می کنیم. برای انجام این کار، سیستمی متشکل از دو معادله را حل می کنیم:

(y = x 3،
(y = 1.

بنابراین، ما x 1 = 1 - حد پایین و x = 2 - حد بالایی داریم.

بنابراین، S = S DACE – S DABE = ʃ 1 2 x 3 dx – 1 = x 4 /4| 1 2 – 1 = (16 – 1)/4 – 1 = 11/4 (واحد مربع).

جواب: 11/4 متر مربع واحدها

مثال 2.

مساحت شکل محدود شده با خطوط y = √x را محاسبه کنید. y = 2; x = 9.

راه حل.

خطوط داده شده شکل ABC را تشکیل می دهند که در بالا توسط نمودار تابع محدود شده است

y = √x، و در زیر نموداری از تابع y = 2 آمده است. برنج. 3.

مساحت مورد نیاز S = ʃ a b (√x – 2) است. بیایید حدود ادغام را پیدا کنیم: b = 9، برای پیدا کردن a، سیستمی از دو معادله را حل می کنیم:

(y = √x،
(y = 2.

بنابراین، ما داریم که x = 4 = a - این حد پایین تر است.

بنابراین، S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 – 2х| 4 9 = (18 - 16/3) - (18 - 8) = 2 2/3 (واحد مربع).

پاسخ: S = 2 2/3 متر مربع. واحدها

مثال 3.

مساحت شکل محدود شده با خطوط y = x 3 - 4x را محاسبه کنید. y = 0; x ≥ 0.

راه حل.

بیایید تابع y = x 3 - 4x را برای x ≥ 0 رسم کنیم. برای انجام این کار، مشتق y را پیدا کنید:

y' = 3x 2 - 4، y' = 0 در x = ± 2/√3 ≈ 1.1 - نقاط بحرانی.

اگر نقاط بحرانی را روی خط اعداد رسم کنیم و علائم مشتق را مرتب کنیم، متوجه می شویم که تابع از صفر به 2/√3 کاهش می یابد و از 2/√3 به اضافه بی نهایت افزایش می یابد. سپس x = 2/√3 حداقل نقطه است، حداقل مقدار تابع y min = -16/(3√3) ≈ -3.

بیایید نقاط تلاقی نمودار را با محورهای مختصات تعیین کنیم:

اگر x = 0، y = 0، به این معنی که A(0؛ 0) نقطه تقاطع با محور Oy است.

اگر y = 0، آنگاه x 3 – 4x = 0 یا x(x 2 – 4) = 0، یا x(x – 2) (x + 2) = 0، از آنجا x 1 = 0، x 2 = 2، x 3 = -2 (مناسب نیست، زیرا x ≥ 0).

نقاط A(0; 0) و B(2; 0) نقاط تقاطع نمودار با محور Ox هستند.

خطوط داده شده شکل OAB را تشکیل می دهند که با هچ کردن نشان داده می شود برنج. 4.

از آنجایی که تابع y = x 3 – 4x مقدار منفی روی (0؛ 2) می گیرد، پس

S = |ʃ 0 2 (x 3 - 4x)dx|.

داریم: ʃ 0 2 (x 3 – 4x)dx =(x 4 /4 – 4x 2 /2)| 0 2 = -4، از این رو S = 4 مربع. واحدها

پاسخ: S = 4 متر مربع. واحدها

مثال 4.

مساحت شکل محدود شده با سهمی y = 2x 2 – 2x + 1، خطوط x = 0، y = 0 و مماس بر این سهمی را در نقطه ای با آبسیسا x 0 = 2 بیابید.

راه حل.

ابتدا، اجازه دهید یک معادله برای مماس به سهمی y = 2x 2 – 2x + 1 در نقطه ای با آبسیسا x0 = 2 ایجاد کنیم.

از آنجایی که مشتق y' = 4x - 2 است، پس برای x 0 = 2، k = y'(2) = 6 دریافت می کنیم.

بیایید ترتیب نقطه مماس را پیدا کنیم: y 0 = 2 2 2 – 2 2 + 1 = 5.

بنابراین، معادله مماس به شکل: y – 5 = 6 (x – 2) یا y = 6x – 7 است.

بیایید شکلی بسازیم که با خطوط محدود شده است:

y = 2x 2 – 2x + 1، y = 0، x = 0، y = 6x – 7.

Г у = 2х 2 – 2х + 1 – سهمی. نقاط تقاطع با محورهای مختصات: A(0; 1) - با محور Oy. با محور Ox - هیچ نقطه تقاطعی وجود ندارد، زیرا معادله 2x 2 – 2x + 1 = 0 هیچ راه حلی ندارد (D< 0). Найдем вершину параболы:

x b = 2/4 = 1/2;

y b = 1/2، یعنی راس نقطه سهمی B دارای مختصات B(1/2؛ 1/2) است.

بنابراین، شکلی که مساحت آن باید تعیین شود با هچ کردن نشان داده می شود برنج. 5.

داریم: S O A B D = S OABC – S ADBC.

بیایید مختصات نقطه D را از شرط پیدا کنیم:

6x – 7 = 0، یعنی. x = 7/6، که به معنای DC = 2 – 7/6 = 5/6 است.

مساحت مثلث DBC را با استفاده از فرمول S ADBC ​​= 1/2 · DC · BC پیدا می کنیم. بدین ترتیب،

S ADBC ​​= 1/2 · 5/6 · 5 = 25/12 مربع واحدها

S OABC = ʃ 0 2 (2x 2 - 2x + 1)dx = (2x 3 /3 - 2x 2 /2 + x)| 0 2 = 10/3 (واحد مربع).

در نهایت به دست می آوریم: S O A B D = S OABC - S ADBC ​​= 10/3 - 25/12 = 5/4 = 1 1/4 (واحد مربع).

پاسخ: S = 1 1/4 متر مربع. واحدها

نمونه هایی را بررسی کرده ایم پیدا کردن مساحت اشکال محدود شده با خطوط داده شده. برای حل موفقیت آمیز چنین مشکلاتی، باید بتوانید خطوط و نمودارهایی از توابع را در یک صفحه بسازید، نقاط تقاطع خطوط را پیدا کنید، فرمولی را برای یافتن مساحت اعمال کنید، که حاکی از توانایی محاسبه انتگرال های خاص است.

وب سایت، هنگام کپی کردن مطالب به طور کامل یا جزئی، پیوند به منبع مورد نیاز است.

عقب به جلو

توجه! پیش نمایش اسلایدها فقط برای اهداف اطلاعاتی است و ممکن است نشان دهنده همه ویژگی های ارائه نباشد. اگر به این کار علاقه مند هستید، لطفا نسخه کامل آن را دانلود کنید.

کلید واژه ها:ذوزنقه منحنی منحنی یکپارچه، ناحیه ای از شکل های محدود شده توسط نیلوفرها

تجهیزات: برد نشانگر، کامپیوتر، پروژکتور چند رسانه ای

نوع درس: درس-سخنرانی

اهداف درس:

• آموزشی:ایجاد فرهنگ کار ذهنی، ایجاد موقعیت موفقیت برای هر دانش آموز و ایجاد انگیزه مثبت برای یادگیری. توانایی صحبت کردن و گوش دادن به دیگران را توسعه دهید.
• در حال توسعه:شکل گیری تفکر مستقل دانش آموز در به کارگیری دانش در موقعیت های مختلف، توانایی تجزیه و تحلیل و نتیجه گیری، توسعه منطق، توسعه توانایی طرح صحیح سؤالات و یافتن پاسخ آنها. بهبود شکل گیری مهارت های محاسباتی، توسعه تفکر دانش آموزان در دوره تکمیل وظایف پیشنهادی، توسعه فرهنگ الگوریتمی.
• آموزشی: ایجاد مفاهیم در مورد ذوزنقه منحنی، در مورد یک انتگرال، برای تسلط بر مهارت های محاسبه مساحت شکل های صفحه

روش تدریس:توضیحی و گویا

در طول کلاس ها

در کلاس های قبلی یاد گرفتیم که مساحت شکل هایی را که مرز آنها خطوط شکسته است محاسبه کنیم. در ریاضیات، روش هایی وجود دارد که به شما امکان می دهد مساحت ارقام محدود شده با منحنی ها را محاسبه کنید. چنین ارقامی ذوزنقه های منحنی نامیده می شوند و مساحت آنها با استفاده از ضد مشتقات محاسبه می شود.

ذوزنقه منحنی ( اسلاید 1)

ذوزنقه منحنی شکلی است که با نمودار یک تابع محدود شده است. sh.m.)، سر راست x = aو x = bو محور x

انواع ذوزنقه های منحنی ( اسلاید 2)

در حال بررسی هستیم انواع مختلفذوزنقه های منحنی و توجه: یکی از خطوط مستقیم به یک نقطه منحط است، نقش تابع محدود کننده توسط خط مستقیم ایفا می شود.

مساحت ذوزنقه منحنی (اسلاید 3)

اجازه دهید انتهای سمت چپ فاصله را درست کنیم آ،و حق ایکسما تغییر خواهیم کرد، یعنی دیوار سمت راست ذوزنقه منحنی را جابجا می کنیم و یک شکل متغیر به دست می آوریم. مساحت یک ذوزنقه منحنی متغیر که توسط نمودار تابع محدود شده است یک ضد مشتق است. افبرای عملکرد f

و در بخش [ آ؛ ب] ناحیه یک ذوزنقه منحنی شکل که توسط تابع تشکیل شده است f،برابر است با افزایش ضد مشتق این تابع:

تمرین 1:

مساحت ذوزنقه منحنی را که با نمودار تابع محدود شده است را بیابید: f(x) = x 2و مستقیم y = 0، x = 1، x = 2.

راه حل: ( طبق اسلاید 3 الگوریتم)

بیایید یک نمودار از تابع و خطوط رسم کنیم

بیایید یکی از ضد مشتقات تابع را پیدا کنیم f(x) = x 2 :

خودآزمایی روی اسلاید

انتگرال

ذوزنقه ای منحنی را در نظر بگیرید که با تابع تعریف شده است fدر بخش [ آ؛ ب]. بیایید این بخش را به چند قسمت تقسیم کنیم. مساحت کل ذوزنقه به مجموع مساحت ذوزنقه های منحنی کوچکتر تقسیم می شود. ( اسلاید 5). هر یک از این ذوزنقه ها را می توان تقریباً یک مستطیل در نظر گرفت. مجموع مساحت این مستطیل ها تصوری تقریبی از کل مساحت ذوزنقه منحنی به دست می دهد. هر چه کوچکتر قسمت را تقسیم کنیم [ آ؛ ب]، هر چه مساحت را با دقت بیشتری محاسبه کنیم.

اجازه دهید این استدلال ها را در قالب فرمول بنویسیم.

تقسیم بخش [ آ؛ ب] به n قسمت با نقطه x 0 = a، x1،…، xn = b.طول k-هفتم با نشان دادن xk = xk – xk-1. بیایید یک جمع بندی کنیم

از نظر هندسی، این مجموع نشان دهنده مساحت شکل سایه دار در شکل است ( sh.m.)

مجموع فرم را مجموع انتگرال تابع می نامند f. (sh.m.)

مجموع انتگرال مقدار تقریبی مساحت را نشان می دهد. مقدار دقیق با عبور از حد به دست می آید. بیایید تصور کنیم که در حال اصلاح پارتیشن بخش [ آ؛ ب] به طوری که طول تمام بخش های کوچک به صفر تمایل دارد. سپس ناحیه شکل تشکیل شده به ناحیه ذوزنقه منحنی نزدیک می شود. می توان گفت مساحت ذوزنقه منحنی برابر با حد مجموع انتگرال است. Sc.t. (sh.m.)یا انتگرال، یعنی

تعریف:

انتگرال یک تابع f(x)از جانب آقبل از بحد مجموع انتگرال نامیده می شود

= (sh.m.)

فرمول نیوتن لایب نیتس

به یاد داریم که حد مجموع انتگرال برابر با مساحت ذوزنقه منحنی است، به این معنی که می توانیم بنویسیم:

Sc.t. = (sh.m.)

از طرف دیگر، مساحت ذوزنقه منحنی با استفاده از فرمول محاسبه می شود

S k.t. (sh.m.)

با مقایسه این فرمول ها به دست می آید:

= (sh.m.)

این برابری فرمول نیوتن لایب نیتس نامیده می شود.

برای سهولت در محاسبه، فرمول به صورت زیر نوشته شده است:

= = (sh.m.)

وظایف: (sh.m.)

1. انتگرال را با استفاده از فرمول نیوتن-لایبنیتس محاسبه کنید: اسلاید 5 را بررسی کنید)

2. انتگرال ها را مطابق نقشه بنویسید ( اسلاید 6 را بررسی کنید)

3. مساحت شکل محدود شده با خطوط را بیابید: y = x 3، y = 0، x = 1، x = 2. ( اسلاید 7)

پیدا کردن مساحت شکل های صفحه ( اسلاید 8)

چگونه می توان مساحت شکل هایی را که ذوزنقه های منحنی نیستند پیدا کرد؟

اجازه دهید دو تابع داده شود که نمودارهای آنها را در اسلاید می بینید . (sh.m.)مساحت شکل سایه دار را پیدا کنید . (sh.m.). آیا شکل مورد بحث ذوزنقه منحنی است؟ چگونه می توان مساحت آن را با استفاده از خاصیت افزایشی مساحت پیدا کرد؟ دو ذوزنقه منحنی را در نظر بگیرید و مساحت دیگری را از مساحت یکی از آنها کم کنید ( sh.m.)

بیایید یک الگوریتم برای یافتن منطقه با استفاده از انیمیشن در یک اسلاید ایجاد کنیم:

1. توابع نمودار
2. نقاط تقاطع نمودارها را روی محور x طرح ریزی کنید
3. شکل به دست آمده را هنگام تلاقی نمودارها سایه بزنید
4. ذوزنقه های منحنی را پیدا کنید که تقاطع یا اتحاد آنها شکل داده شده است.
5. مساحت هر یک از آنها را محاسبه کنید
6. تفاوت یا مجموع مساحت ها را پیدا کنید

تکلیف شفاهی: نحوه بدست آوردن مساحت یک شکل سایه دار (با استفاده از انیمیشن بگویید، اسلاید 8 و 9)

مشق شب:از طریق یادداشت ها، شماره 353 (الف)، شماره 364 (الف) کار کنید.

کتابشناسی - فهرست کتب

1. جبر و آغاز تجزیه و تحلیل: کتاب درسی برای کلاس های 9-11 مدرسه عصر (نوبت) / ویرایش. G.D. گلیزر. - م: روشنگری، 1983.
2. باشماکوف M.I. جبر و آغاز تجزیه و تحلیل: کتاب درسی برای کلاس های 10-11 دبیرستان / باشماکوف M.I. - م: روشنگری، 1991.
3. باشماکوف M.I. ریاضیات: کتاب درسی برای مؤسسات آغازین. و چهارشنبه پروفسور تحصیلات / M.I. باشماکوف - م: آکادمی، 2010.
4. کولموگروف A.N. جبر و آغاز تجزیه و تحلیل: کتاب درسی برای پایه های 10-11. موسسات آموزشی / A.N. Kolmogorov. - م: آموزش، 2010.
5. Ostrovsky S.L. چگونه برای یک درس ارائه دهیم؟/ S.L. استروفسکی. - م.: اول سپتامبر 2010.

مساحت شکل محدود شده با خطوط را محاسبه کنید.

راه حل.

یافتن نقاط تقاطع خطوط داده شده. برای انجام این کار، ما سیستم معادلات را حل می کنیم:

برای یافتن آبسیسا نقاط تلاقی خطوط داده شده، معادله را حل می کنیم:

ما پیدا می کنیم: ایکس 1 = -2, ایکس 2 = 4.

بنابراین، این خطوط که یک سهمی و یک خط مستقیم هستند، در نقاطی قطع می شوند آ(-2; 0), ب(4; 6).

این خطوط یک شکل بسته را تشکیل می دهند که مساحت آن با استفاده از فرمول بالا محاسبه می شود:

با استفاده از فرمول نیوتن-لایبنیتس متوجه می شویم:

ناحیه ای که با بیضی محدود شده است را پیدا کنید.

راه حل.

از معادله بیضی برای ربع اول داریم. از اینجا با استفاده از فرمول دریافت می کنیم

بیایید جایگزینی را اعمال کنیم ایکس = آگناه تی, dx = آ cos تی dt. محدودیت های جدید ادغام تی = α و تی = β از معادلات 0 = تعیین می شود آگناه تی, آ = آگناه تی. می توان قرار داد α = 0 و β = π /2.

یک چهارم مساحت مورد نیاز را پیدا کنید

از اینجا اس = πb.

مساحت شکل محدود شده با خطوط را پیدا کنیدy = - ایکس 2 + ایکس + 4 وy = - ایکس + 1.

راه حل.

بیایید نقاط تلاقی خطوط را پیدا کنیم y = -ایکس 2 + ایکس + 4, y = -ایکس+ 1، معادل کردن مختصات خطوط: - ایکس 2 + ایکس + 4 = -ایکس+ 1 یا ایکس 2 - 2ایکس- 3 = 0. یافتن ریشه ها ایکس 1 = -1, ایکس 2 = 3 و ترتیب مربوط به آنها y 1 = 2, y 2 = -2.

با استفاده از فرمول مساحت یک شکل، به دست می آوریم

مساحت محصور شده توسط سهمی را تعیین کنیدy = ایکس 2 + 1 و مستقیمایکس + y = 3.

راه حل.

حل یک سیستم معادلات

آبسیسا نقاط تقاطع را پیدا کنید ایکس 1 = -2 و ایکس 2 = 1.

باور کردن y 2 = 3 - ایکسو y 1 = ایکس 2 + 1، بر اساس فرمولی که به دست می آوریم

مساحت موجود در lemniscate برنولی را محاسبه کنیدr 2 = آ 2 cos 2 φ .

راه حل.

در سیستم مختصات قطبی، مساحت یک شکل محدود به یک قوس منحنی است r = f(φ ) و دو شعاع قطبی φ 1 = ʅ و φ 2 = ʆ ، با انتگرال بیان خواهد شد

با توجه به تقارن منحنی ابتدا یک چهارم مساحت مورد نیاز را تعیین می کنیم

بنابراین، کل مساحت برابر است با اس = آ 2 .

طول قوس سیارک را محاسبه کنیدایکس 2/3 + y 2/3 = آ 2/3 .

راه حل.

اجازه دهید معادله سیارک را به شکل بنویسیم

(ایکس 1/3) 2 + (y 1/3) 2 = (آ 1/3) 2 .

بگذاریم ایکس 1/3 = آ 1/3 cos تی, y 1/3 = آ 1/3 گناه تی.

از اینجا معادلات پارامتری سیارک را بدست می آوریم

ایکس = آ cos 3 تی, y = آگناه 3 تی, (*)

جایی که 0 ≤ تی ≤ 2π .

به دلیل تقارن منحنی (*) کافی است یک چهارم طول قوس را پیدا کنید. L، مربوط به تغییر پارامتر است تیاز 0 تا π /2.

ما گرفتیم

dx = -3آ cos 2 تیگناه t dt, دو = 3آگناه 2 تی cos t dt.

از اینجا پیدا می کنیم

ادغام عبارت حاصل از 0 به π /2، می گیریم

از اینجا L = 6آ.

ناحیه محصور شده توسط مارپیچ ارشمیدس را پیدا کنیدr = aφ و دو بردار شعاع که با زوایای قطبی مطابقت دارندφ 1 وφ 2 (φ 1 < φ 2 ).

راه حل.

ناحیه ای که توسط یک منحنی محصور شده است r = f(φ ) با فرمول، که در آن محاسبه می شود α و β - محدودیت های تغییر زاویه قطبی.

بنابراین، ما دریافت می کنیم

(*)

از (*) چنین بر می آید که ناحیه محدود شده توسط محور قطبی و اولین چرخش مارپیچ ارشمیدس ( φ 1 = 0; φ 2 = 2π ):

به طور مشابه، منطقه محدود شده توسط محور قطبی و پیچ دوم مارپیچ ارشمیدس ( φ 1 = 2π ; φ 2 = 4π ):

مساحت مورد نیاز برابر است با اختلاف این مناطق

حجم جسمی را که با چرخش حول یک محور به دست می آید محاسبه کنیدگاو نر ارقام محدود شده توسط سهمیy = ایکس 2 وایکس = y 2 .

راه حل.

بیایید سیستم معادلات را حل کنیم

و می گیریم ایکس 1 = 0, ایکس 2 = 1, y 1 = 0, y 2 = 1، از آنجا نقاط تقاطع منحنی ها O(0; 0), ب(یازده). همانطور که در شکل مشاهده می شود، حجم مورد نیاز یک بدنه چرخشی برابر است با اختلاف بین دو حجمی که از چرخش حول یک محور تشکیل می شود. گاو نرذوزنقه های منحنی O.C.B.A.و ODBA:

مساحت محصور شده توسط یک محور را محاسبه کنیدگاو نر و سینوسیy = گناهایکس در بخش ها: الف)؛ ب) .

راه حل.

الف) روی قطعه تابع sin ایکسعلامت را حفظ می کند و بنابراین طبق فرمول، با فرض y= گناه ایکس، ما پیدا می کنیم

ب) در قطعه، تابع sin ایکسعلامت را تغییر می دهد برای حل صحیح مشکل، لازم است بخش را به دو قسمت تقسیم کنیم و [ π , 2π ]، که در هر کدام تابع علامت خود را حفظ می کند.

طبق قاعده علائم، در بخش [ π , 2π ] منطقه با علامت منفی گرفته شده است.

در نتیجه مساحت مورد نیاز برابر است با

حجم جسم محدود شده با سطحی که از چرخش یک بیضی به دست می آید را تعیین کنیدحول محور اصلیآ .

راه حل.

با توجه به متقارن بودن بیضی نسبت به محورهای مختصات، کافی است حجمی را که از چرخش حول محور تشکیل می شود، پیدا کنیم. گاو نرحوزه OABبرابر با یک چهارم مساحت بیضی است و نتیجه را دو برابر کنید.

اجازه دهید حجم یک بدنه چرخش را با نشان دهیم V ایکس; سپس بر اساس فرمولی که داریم 0 و آ- ابسیسا از نقاط بو آ. از معادله بیضی پیدا می کنیم. از اینجا

بنابراین، حجم مورد نیاز برابر است با. (زمانی که بیضی حول محور فرعی می چرخد ب، حجم بدن برابر است با )

ناحیه محدود شده با سهمی را پیدا کنیدy 2 = 2 px وایکس 2 = 2 py .

راه حل.

ابتدا مختصات نقاط تقاطع سهمی ها را برای تعیین بخش انتگرال گیری پیدا می کنیم. با تبدیل معادلات اصلی به دست می آوریم و . با برابر کردن این مقادیر، یا می گیریم ایکس 4 - 8پ 3 ایکس = 0.

ایکس 4 - 8پ 3 ایکس = ایکس(ایکس 3 - 8پ 3) = ایکس(ایکس - 2پ)(ایکس 2 + 2px + 4پ 2) = 0.

پیدا کردن ریشه معادلات:

با توجه به اینکه نکته آتقاطع سهمی ها در ربع اول است، سپس حدود ادغام ایکس= 0 و ایکس = 2پ.

با استفاده از فرمول ناحیه مورد نیاز را پیدا می کنیم